Lecture 1
Engineering vs Mathematics
Truth + Proof
Truth + Proof + Axioms
Euclid's Elements
The Parallel Postulate
Truth + Proof
Truth + Proof + Axioms
Euclid's Elements
The Parallel Postulate

Lecture 2
Proposition I.1
Platonic Solids
Hyperbolic Geometry
Parallel Postulate
Platonic Solids
Hyperbolic Geometry
Parallel Postulate
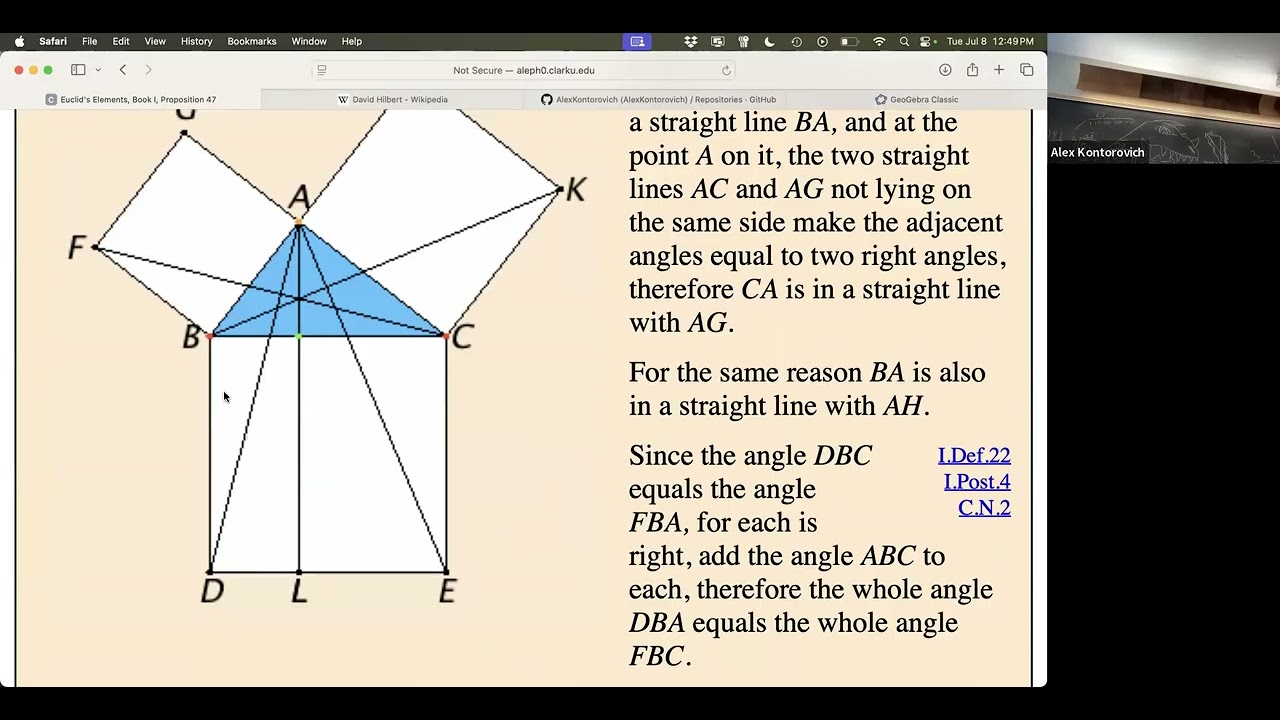
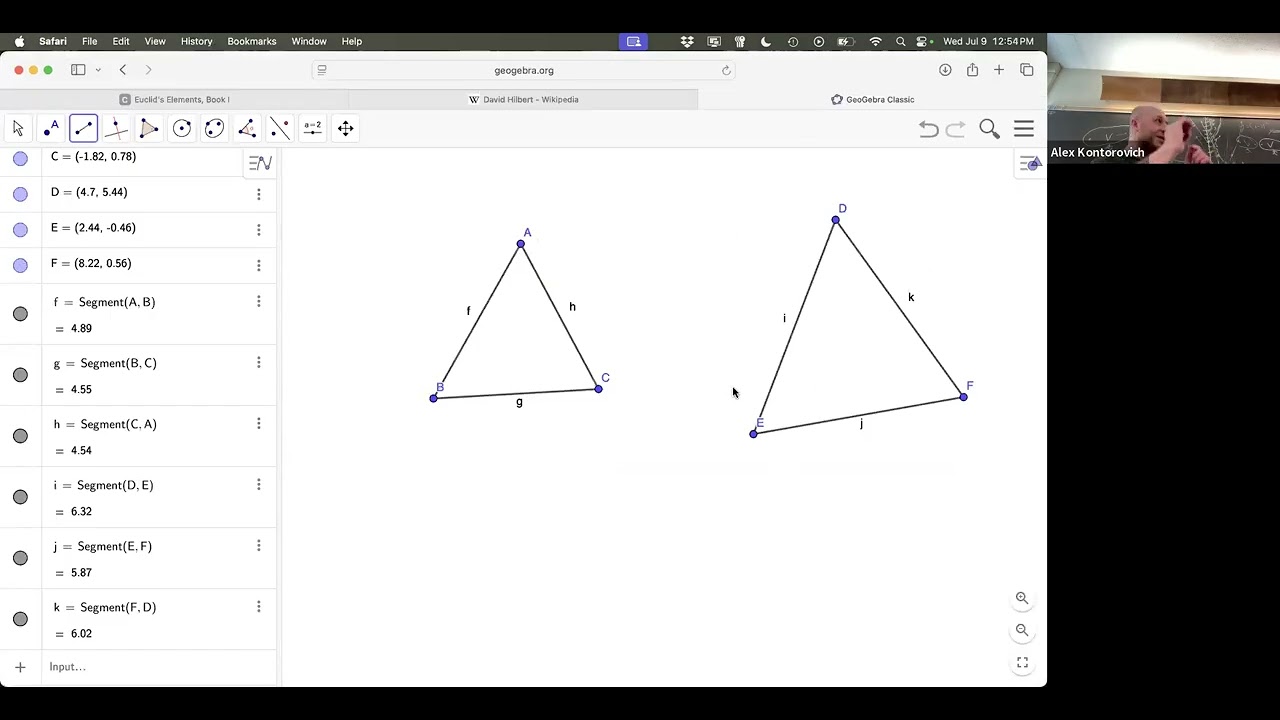
Lecture 3
In Non-Euclidean Geometry, AAA Implies Congruence
Gap in Euclid's Prop I.1
David Hilbert's Ideas on Formalization
Undefined Terms
Beginning Formalization
Gap in Euclid's Prop I.1
David Hilbert's Ideas on Formalization
Undefined Terms
Beginning Formalization
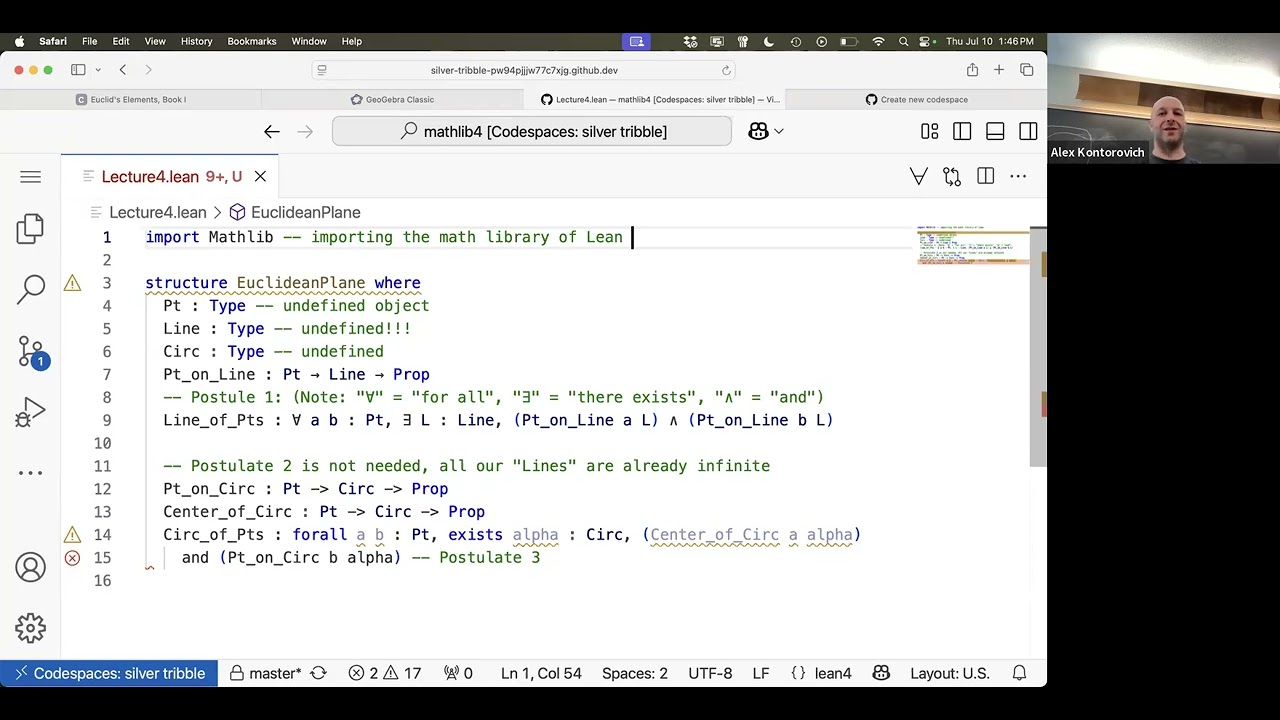
Lecture 4
Setting up Formal Euclidean Plane
Equilateral Triangle
Developing Axioms
Equilateral Triangle
Developing Axioms